Skip to main content

Arbitrage Guide

Overview​

The Yield Basis system maintains 2x leverage through two key mechanisms:

  1. AMM (Automated Market Maker): Uses mathematical bonding curves to maintain constant leverage
  2. Virtual Pool: Enables arbitrage without requiring users to handle LP tokens directly

Arbitrage opportunities arise when:

  • AMM prices deviate from Curve pool prices
  • Leverage ratios drift from the target 2x

How the VirtualPool routes trades​

The VirtualPool enables arbitrage between STABLECOIN (i=0) and ASSET (i=1) using the Curve pool and the market's LEVAMM, facilitated by a flash loan of the stablecoin from Factory.flash().

  • Flash loan covers only the opposite leg: you supply the input token (BTC or crvUSD); the VirtualPool flash-borrows stablecoin (crvUSD) internally.
  • No LP handling: LP mint/burn is internal—users never receive LP tokens.
  • Safety & leverage: The LEVAMM enforces a constant-leverage curve (L≈2× in YieldBasis) with a safety band; VirtualPool just routes trades through it.
  • Protection: Always quote with get_dy() and set min_out to avoid unprofitable fills.

Stable → Asset Swaps (i=0, j=1):

  1. User sends crvUSD to VirtualPool.
  2. VirtualPool takes a stablecoin flash loan.
  3. VirtualPool buys LP from the AMM: AMM.exchange(0, 1, user_stable*(1−ROUNDING_DISCOUNT)+flash, 0).
  4. VirtualPool removes liquidity in the Curve pool: POOL.remove_liquidity(lp_amount, [0,0]).
  5. VirtualPool repays the flash loan from the stable side.
  6. Remaining asset is transferred to the user.

Asset → Stable Swaps (i=1, j=0):

  1. User sends BTC to VirtualPool.
  2. VirtualPool takes a stablecoin flash loan.
  3. VirtualPool mints LP in the Curve pool: POOL.add_liquidity([flash, user_asset], 0).
  4. VirtualPool sells LP to the AMM: AMM.exchange(1, 0, lp_amount, 0).
  5. VirtualPool repays the flash loan.
  6. Remaining stablecoin is transferred to the user.

The flash callback enforces that the caller is the configured flash provider and the borrowed token is the stablecoin. A small ROUNDING_DISCOUNT is applied on stable->asset quotes to avoid over-estimation.

Mathematical Foundation​

Leverage Calculation​

The AMM maintains leverage through a bonding curve:

# AMM.vy
def get_x0(p_o: uint256, collateral: uint256, debt: uint256, safe_limits: bool) -> uint256:
    # x0 represents the virtual balance maintaining 2x leverage
    # p_o = oracle price
    # collateral = LP token amount (the AMM's collateral)
    # debt = stablecoin debt (interest-accrued where applicable)
    # safe_limits = enforce safety band when True
  • Target Leverage: 2x (50% debt-to-value ratio)
  • Price Increase: DTV < 50% -> Arbitrageurs add debt to restore leverage
  • Price Decrease: DTV > 50% -> Arbitrageurs reduce debt to restore leverage

How the code creates (and enforces) arbitrage back to ~2×​

The LEVAMM prices trades on a constant-leverage curve anchored to the oracle, and it only accepts trades that move the system toward the safe region around 2×. When debt-to-value (DTV) drifts away from ~50%, the AMM's quoted price for LP ↔ crvUSD shifts so that an external route (Curve mint/burn) + AMM.exchange becomes profitable. VirtualPool packages that route with a flash-loaned stable leg so arbitrageurs never touch LP.

  • State & price basis

    • get_state() exposes (collateral, debt, x0) where collateral is LP amount and debt is interest-accrued.
    • get_p() derives the AMM price (stable per LP) from the oracle and current state: it uses get_x0(p_o, collateral, debt, False) internally.

  • Safety band (keeps DTV sane)

    • get_x0(p_o, collateral, debt, safe_limits=True) enforces min/max debt vs oracle collateral value (for L=2×, roughly 6.25%–53.125% of value).

    • Every trade ends with:

      # AMM.exchange(...)
      assert self.get_x0(p_o, collateral_after, debt_after, True) >= x0_before, "Bad final state"

      This rejects trades that would leave safe bounds or move the state toward the "untradable" region. In practice it nudges the system back toward the 2× area.

  • Directional inventory changes

    • Stable -> LP (exchange(0,1,…)): reduces debt, reduces collateral (AMM sells LP for stables to the trader). Used to decrease DTV when the system is over-leveraged.
    • LP -> Stable (exchange(1,0,…)): increases debt, increases collateral (AMM buys LP from the trader, paying stables). Used to increase DTV when the system is under-leveraged. These updates are explicit in exchange(...) after computing out_amount.

Why the price becomes favorable (how the spread appears)​

  • Quotes come from the curve, not from the pool: get_dy(i, j, in_amount) (and its on-chain twin inside exchange(...)) uses the constant-leverage geometry (via x0, x_initial) and applies fee. The resulting marginal price moves with DTV.

    • If the AMM is under-leveraged (DTV < 50%), it bids LP aggressively in get_dy(1->0) (LP->crvUSD). Selling LP to the AMM and redeeming/creating LP via Curve becomes attractive -> arbitrage adds debt (pushes DTV up).
    • If the AMM is over-leveraged (DTV > 50%), it offers LP cheaply in get_dy(0->1) (crvUSD->LP). Buying LP from the AMM and burning it to underlying via Curve becomes attractive -> arbitrage reduces debt (pushes DTV down).

  • Oracle-anchored pricing: get_p() and get_x0() both use the pool's oracle price (PRICE_ORACLE_CONTRACT.price() / price_w()), so quoted trades react to exogenous price moves. After a price jump/drop, the AMM quote shifts immediately, creating the spread vs the Curve mint/burn price that VirtualPool exploits.

  • Fees & rounding: Each quote applies fee (AMM) and, on the VirtualPool's stable->asset path, a small ROUNDING_DISCOUNT to avoid over-estimating user input. These don't create the opportunity, but they set the threshold where arbitrage becomes profitable after gas/flash costs.

How VirtualPool turns the quote into an executable arb​

VirtualPool's exchange(i, j, in_amount, min_out) wraps the profitable side without LP custody:

  • Stable → Asset Swaps (crvUSD->BTC): flash-borrow stable -> AMM.exchange(0,1, …) (stable->LP) -> POOL.remove_liquidity(lp, [0,0]) -> repay flash from the stable side -> user receives asset.
  • Asset → Stable Swaps (BTC->crvUSD): flash-borrow stable -> POOL.add_liquidity([flash, asset], 0) (mint LP) -> AMM.exchange(1,0, lp, 0) (LP->stable) -> repay flash -> user receives crvUSD.

Because the AMM quote improves in the direction that restores 2×, the combined AMM+Curve route yields positive edge whenever DTV has drifted enough to cover fees. The final assert in AMM.exchange guarantees that any executed trade has moved the state toward safety, never away.

Relevant functions to read:

Arbitrage Profit Calculation​

Use VirtualPool.get_dy() to calculate expected output tokens:

📋 VirtualPool.get_dy() Source Code
# i=0: crvUSD -> BTC, i=1: BTC -> crvUSD
out = VirtualPool.get_dy(i, j, in_amount)
@internal
@view
def _calculate(i: uint256, in_amount: uint256, only_flash: bool) -> (uint256, uint256):
    stables_in_pool: uint256 = staticcall POOL.balances(0)
    out_amount: uint256 = 0

    if i == 0:
        state: AMMState = staticcall AMM.get_state()
        pool_supply: uint256 = staticcall POOL.totalSupply()
        fee: uint256 = staticcall AMM.fee()
        r0fee: uint256 = stables_in_pool * (10**18 - fee) // pool_supply

        # Solving quadratic eqn instead of calling the AMM b/c we have a special case
        b: uint256 = state.x0 - state.debt + in_amount - r0fee * state.collateral // 10**18
        D: uint256 = b**2 + 4 * state.collateral * r0fee // 10**18 * in_amount
        flash_amount: uint256 = (isqrt(D) - b) // 2  # We received this withdrawing from the pool

        if not only_flash:
            crypto_in_pool: uint256 = staticcall POOL.balances(1)
            out_amount = flash_amount * crypto_in_pool // stables_in_pool
        # Withdrawal was ideally balanced
        return out_amount, flash_amount

    else:
        crypto_in_pool: uint256 = staticcall POOL.balances(1)
        flash_amount: uint256 = in_amount * stables_in_pool // crypto_in_pool
        if not only_flash:
            pool_supply: uint256 = staticcall POOL.totalSupply()
            lp_amount: uint256 = pool_supply * in_amount // crypto_in_pool
            out_amount = staticcall AMM.get_dy(1, 0, lp_amount) - flash_amount
        return out_amount, flash_amount
# Check expected crvUSD output for BTC input
expected_crvusd = VirtualPool.get_dy(1, 0, 0.1 * 10**8)  # BTC -> crvUSD

# Check expected BTC output for crvUSD input
expected_btc = VirtualPool.get_dy(0, 1, 10_000 * 10**18)  # crvUSD -> BTC

Important: The VirtualPool handles the entire arbitrage process internally:

  1. Takes your input (BTC or crvUSD)
  2. Executes LP ↔ crvUSD trades using flash loans
  3. Returns the entire output amount in the output token (crvUSD or BTC)

Note: get_dy() already reflects the full internal route (AMM + Curve + flash repay). No LP math needed.

See this Google Colab notebook for a working example of calculating expected outputs.

Arbitrage Scenarios​

Scenario 1: BTC Price Increases​

Arbitrage Flow when price increasesArbitrage Flow when price increases

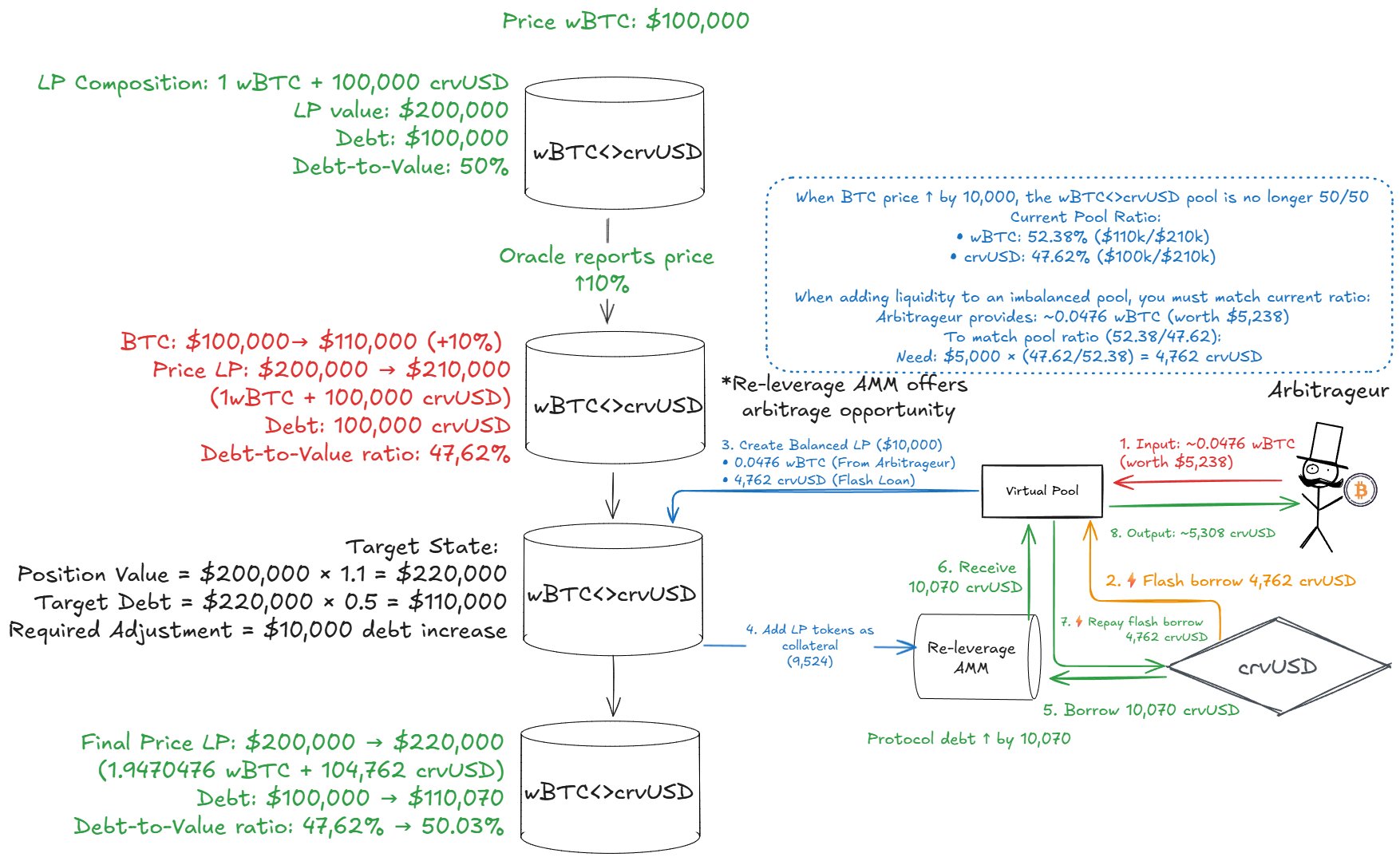
Example Arbitrage Flow During Price Increases

BTC price increases from $100,000 to $110,000 (+10%)

Initial State:

  • LP Composition: 1 BTC + 100,000 crvUSD
  • LP Value: $200,000
  • Debt: $100,000
  • Debt-to-Value: 50%

After Price Increase:

  • LP Value: $210,000 (1 BTC × $110,000 + 100,000 crvUSD)
  • Debt: $100,000 (unchanged)
  • Debt-to-Value: 47.62% (below target 50%)

Why Arbitrage Opportunity Exists: The AMM's bonding curve pricing creates an incentive when DTV ≠ 50%:

  • Current DTV: 47.62% (under-leveraged)
  • Target DTV: 50% (2x leverage)
  • AMM Trading: AMM trades LP tokens ↔ crvUSD
  • Arbitrage Opportunity: When under-leveraged, AMM offers better prices for selling LP tokens (getting crvUSD)
  • Economic Incentive: Arbitrageurs can profit by selling LP tokens to the AMM, which reduces the AMM's LP position and increases its crvUSD, restoring 50% DTV

Arbitrage Process: Note: The Virtual Pool handles all the complex logic internally. Arbitrageurs simply call VirtualPool.exchange().

Internal Steps (handled automatically by Virtual Pool):

  1. Input: BTC to Virtual Pool via VirtualPool.exchange(1, 0, asset_in, min_out)
  2. Flash borrow: stablecoin from Factory.flash()
  3. Mint LP: POOL.add_liquidity([flash_stable, asset_in], 0) -> mint LP
  4. Sell LP: AMM.exchange(1, 0, lp_amount, 0) -> LP -> stable
  5. Repay flash: from stable side
  6. Output: remaining stablecoin (crvUSD) -> arbitrageur

Scenario 2: BTC Price Decreases​

Arbitrage Flow when price decreasesArbitrage Flow when price decreases

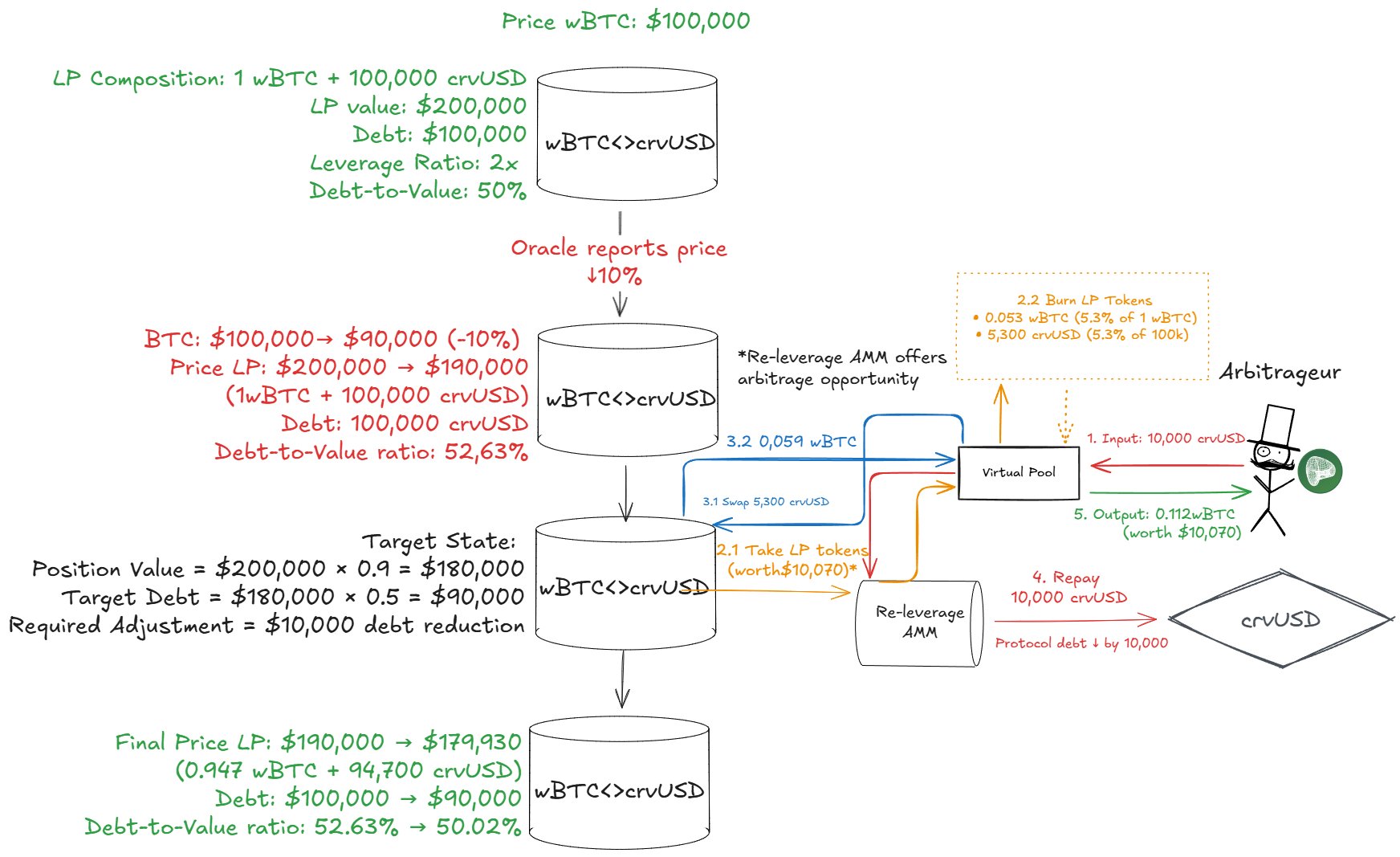
Example Arbitrage Flow During Price Decrease

BTC price decreases from $100,000 to $90,000 (-10%)

Initial State:

  • LP Composition: 1 BTC + 100,000 crvUSD
  • LP Value: $200,000
  • Debt: $100,000
  • Debt-to-Value: 50%

After Price Decrease:

  • LP Value: $190,000 (1 BTC × $90,000 + 100,000 crvUSD)
  • Debt: $100,000 (unchanged)
  • Debt-to-Value: 52.63% (above target 50%)

Why Arbitrage Opportunity Exists: The AMM's bonding curve pricing creates an incentive when DTV ≠ 50%:

  • Current DTV: 52.63% (over-leveraged)
  • Target DTV: 50% (2x leverage)
  • AMM Trading: AMM trades LP tokens ↔ crvUSD
  • Arbitrage Opportunity: When over-leveraged, AMM offers better prices for buying LP tokens (spending crvUSD)
  • Economic Incentive: Arbitrageurs can profit by buying LP tokens from the AMM, which increases the AMM's LP position and reduces its crvUSD, restoring 50% DTV

Arbitrage Process: Note: The Virtual Pool handles all the complex logic internally. Arbitrageurs simply call VirtualPool.exchange().

Internal Steps (handled automatically by Virtual Pool):

  1. Input: crvUSD to Virtual Pool via VirtualPool.exchange(0, 1, stable_in, min_out)
  2. Flash borrow: stablecoin from Factory.flash()
  3. Buy LP: AMM.exchange(0, 1, stable_in*(1-ROUNDING_DISCOUNT) + flash, 0) -> stable -> LP
  4. Remove liquidity: POOL.remove_liquidity(lp_amount, [0, 0]) -> LP -> (stable, asset)
  5. Repay flash: from stable side
  6. Output: remaining asset (BTC) -> arbitrageur

How to Execute Arbitrage​

Step 1: Check for Arbitrage Opportunities​

Price Comparison:

  • Get AMM LP price: AMM.get_p() - returns stable per LP (see AMM documentation)
  • Get Curve LP price: POOL.lp_price() (or POOL.get_virtual_price()) - returns stable per LP
  • Compare LP prices to identify opportunities

Leverage Check:

  • Get current AMM state: AMM.get_state() - returns (collateral, debt, x0) (see AMM documentation)
  • Calculate current DTV ratio: debt / (collateral * price) (use the oracle price, not get_p())
  • Target DTV should be 50% (2x leverage)

Step 2: Calculate Expected Profit​

For Price Increase Arbitrage:

# Calculate expected output from Virtual Pool
expected_output = VirtualPool.get_dy(1, 0, btc_amount)
profit = expected_output - btc_amount * market_price

For Price Decrease Arbitrage:

# Calculate expected output from Virtual Pool
expected_output = VirtualPool.get_dy(0, 1, stablecoin_amount)
profit = expected_output - stablecoin_amount / market_price

Step 3: Execute Arbitrage​

Price Increase (BTC -> crvUSD):

# Call Virtual Pool exchange
VirtualPool.exchange(1, 0, btc_amount, min_out_amount)

Price Decrease (crvUSD -> BTC):

# Call Virtual Pool exchange
VirtualPool.exchange(0, 1, stablecoin_amount, min_out_amount)

Key Functions for Arbitrage​

VirtualPool Functions​

get_dy() - Expected Output:

# Returns expected output in either stablecoin or asset
# i=0: stablecoin, i=1: asset
expected_output = VirtualPool.get_dy(i, j, in_amount)

coins() - Token Addresses:

# Get token addresses
stablecoin = VirtualPool.coins(0)  # crvUSD address
asset = VirtualPool.coins(1)      # BTC address

AMM Functions​

get_state() - Current State:

# Returns (collateral, debt, x0)
state = AMM.get_state()
collateral = state[0]  # LP token amount
debt = state[1]        # Interest-accrued debt
x0 = state[2]          # Virtual balance for 2x leverage

Calculate Current DTV Ratio:

def calculate_dtv_ratio():
    state = AMM.get_state()                 # collateral (LP), debt, x0
    p_o = PRICE_ORACLE_CONTRACT.price()     # oracle price
    # Include the same precision scaling you use elsewhere if needed
    collateral_value = p_o * state.collateral
    dtv = state.debt * 10**18 // collateral_value
    return dtv  # ~5e17 (50%) at target