Advanced Concepts & Economics

This page goes beyond “How it Works” and explains the machinery, incentives, and economics that make YieldBasis function at scale.

Math-heavy details live in the Math Primer leverage derivation (√p → p), Rebalancing‑AMM invariant & x₀, flash‑loan sizing (φ), net APR equation, and the admin-fee curve.

---

1. System Architecture (High‑Level)

YieldBasis is a stack of coordinated contracts built around Curve.

Component	What it does	Who touches it?
Curve Cryptoswap Pools (BTC/crvUSD)	Hold BTC & crvUSD, generate trading fees	Anyone (swappers, arbers, protocol)
Rebalancing‑AMM	Prices LP ↔ crvUSD to keep leverage at 2×	Only via the VirtualPool (no UI)
VirtualPool	Bundles flash loans, LP mint/burn, debt ops into 1 tx	Arbitrageurs call a single swap()
YB crvUSD CDP Line	Mints/repays crvUSD against LP collateral	Protocol only
ybBTC Token	Receipt token for user deposits/withdrawals	Users
veYB / Staking	Governance & fee receiver	Stakers / governance

1.1 Data & Value Flows

An on‑chain BTC/USD oracle feeds the Rebalancing‑AMM so it can compute the anchor state and the exact debt target (always 50% of LP value). When a user deposits BTC, the protocol flash‑borrows the same USD value in crvUSD, adds both assets to the Curve pool to mint LP, posts that LP as collateral in an isolated crvUSD CDP, then borrows crvUSD against it to repay the flash loan—leaving a 2× leveraged (50/50) position. Trading fees accrue in the Curve pool and, when harvested, are routed via the YB admin‑fee split to unstaked LPs and veYB.

Separately, the crvUSD debt accrues interest at a governance‑set, YieldBasis‑specific rate; that interest is recycled, roughly half funds the Rebalancing Subsidy (so arbitrageurs keep leverage perfect) and the remainder flows through the same admin‑fee split to unstaked LPs and veYB.

Whenever the debt/value ratio drifts from 50%, the Rebalancing‑AMM exposes a tiny price difference; arbitrageurs take a single swap through the VirtualPool, which atomically flash‑borrows, mints/burns LP, mints/repays crvUSD, settles the flash loan, and pockets the difference, restoring 2× leverage without user intervention.

1.2 High‑Level Sequence

1. User deposits BTC -> receives ybBTC.
2. The contract flash‑borrows crvUSD equal to the BTC’s USD value.
3. It adds BTC + crvUSD as liquidity to the Curve Cryptoswap pool and mints LP tokens (spot price remains unchanged because liquidity is added in balanced proportion).
4. Those LP tokens are used as collateral in the YB crvUSD CDP.
5. The protocol borrows crvUSD against that LP and repays the flash loan, leaving a net 50% debt / 50% equity position (2× leverage).
6. Going forward, if BTC moves, arbitrageurs rebalance via the VirtualPool (and Rebalancing-AMM) so the debt-to-value ratio stays at 50% (2x leverage).

1.3 Oracle & Pricing Inputs

The Rebalancing‑AMM needs a single BTC/USD reference price (p₀) to know what “50% debt” should be and to center its pricing curve. p₀ feeds the calculations for the anchoring term x₀(p₀) and the ideal debt level.

---

2. Leverage Engine

YieldBasis fixes leverage at 2×. Practically: debt is always 50% of the LP’s USD value. Curve LP value grows roughly like $\sqrt{price}$. By keeping a constant compounding leverage of 2×, the protocol “squares” that curve so your position scales with price itself. That gives you linear BTC exposure and no impermanent loss versus simply holding BTC.

Math reference: The leverage identity V_* ∝ V_c^L and why picking L = 2 turns √p → p are derived in Math Primer §2 (Eq. 2–4).

Why exactly 2×?

• It’s the precise leverage that turns $\sqrt{p}$ into p.
• At 50% debt, the LP’s USD side is usually enough to close the loan cleanly at any time, as both the USD portion and the loan comprise 50% of the position value.
• Operationally, “keep debt at 50%” is simple to monitor and rebalance.

What if leverage were higher than 2×?

• Then your position would scale faster than BTC ($p^\frac{L}{2}$ for other $L$). You’d outperform on the way up but underperform on the way down — i.e. you’ve reintroduced “divergence” versus a plain 1 BTC hold (a leverage-style loss, not the classic AMM IL, but still a mismatch from the goal of removing IL).
• It also increases liquidation risk and subsidy requirements (more debt to maintain, more to repay when price falls).

So locking leverage at 2× is the sweet spot: linear BTC tracking, no AMM IL, manageable debt, and clean unwind mechanics.

2.1 How it’s kept at 50%

When BTC moves, the LP value changes:

• Price up: LP value ↑, debt fixed -> debt/value < 50% -> protocol adds debt to regain 50% (mints crvUSD, mints LP).
• Price down: LP value ↓, debt fixed -> debt/value > 50% -> protocol repays debt to regain 50% (redeems LP for crvUSD).

The Rebalancing‑AMM exposes a tiny profit so arbitrageurs do this in one swap via the VirtualPool.

For the full arbitrage flow please see section 4. Rebalancing Flow.

Possible Edge Cases to the Rebalancing Flow:

• Very fast moves can widen spreads; it may take a few swaps to hit exactly 50%.
• Over‑tight Curve concentration can cause temporary drawdowns if rebalancing “breaks” (see §8).
• If crvUSD wobbles around $1, the ratio skews briefly; the oracle smooths this out.

Full derivations (e.g. why value ∝ collateral^L) are in the Math Primer.

---

3. Rebalancing Flow

YieldBasis keeps debt / LP value = 50% (2× leverage) by exposing an arbitrage opportunity whenever the ratio moves. Two internal pieces make this work:

• Rebalancing‑AMM – holds LP tokens on one side and tracks crvUSD debt on the other; it shifts price so trades push the ratio back to 50%.
• VirtualPool – a router that wraps flash loans, Curve LP mint/burn, and CDP mint/repay into one atomic swap the arbitrageur invokes. It is essentially the interface for arbitrageurs.

3.1 When is a rebalance needed?

As soon as BTC moves, LP value changes but debt doesn’t:

• BTC up: LP value ↑, debt fixed -> debt / value < 0.5 -> need more debt
• BTC down: LP value ↓, debt fixed -> debt / value > 0.5 -> need less debt

Approximate target change in debt:

Δd ≈ 0.5 * (LP_value_new - LP_value_old)

Math reference: The quadratic for the flash‑loan amount φ (whitepaper Eq. 39–41) is shown in Math Primer §3.5.

3.2 Arbitrage Walkthrough — Where the Profit Actually Is

The arbitrage opportunity lives in the Rebalancing‑AMM price for LP <-> crvUSD.

• Debt too low (BTC up): LP is quoted expensive in crvUSD -> pay crvUSD, get LP, unwrap to BTC + crvUSD, repay flash loan, keep the spread.
• Debt too high (BTC down): LP is cheap -> buy LP with crvUSD, unwrap, repay debt, pocket leftover BTC.

The VirtualPool bundles every leg (flash‑borrow, LP mint/burn, CDP mint/repay) into one atomic swap(). The arbitrageur still makes only a single call.

Example: BTC +10% (need to add debt)

Before move
LP ≈ $200k (1 wBTC + 100k crvUSD), debt = 100k crvUSD -> 50% debt / value.

After move
BTC -> $110k, LP ≈ $210k, debt still 100k -> debt / value ≈ 47.6% (< 50%).
Rebalancing‑AMM now quotes LP at a premium in crvUSD.

Arb trade:

• Arb sends ~0.0476 wBTC (~$5,238) to the VirtualPool.
• VirtualPool flash‑borrows ~4,762 crvUSD to form a balanced $10k LP mint in Curve (keeps Curve spot unchanged).
• Sells that LP to the Rebalancing‑AMM for ~$10,070 crvUSD.
• Repays the flash loan (4,762 crvUSD) and keeps ~$308 crvUSD as profit.
• Protocol debt increases by ~$10,070 -> back near 50% again.

End state
LP ≈ $220k, debt ≈ $110k -> debt / value ≈ 50%. Leverage restored; arb walks away paid.

Example: BTC –10% (need to reduce debt)

Before move
Same starting point: LP ≈ $200k, debt = 100k -> 50% debt / value.

After move
BTC -> $90k, LP ≈ $190k, debt still 100k -> debt / value ≈ 52.6% (> 50%).
Rebalancing‑AMM now quotes LP at a discount.

Arb trade:

• Arb inputs 10,000 crvUSD to the VirtualPool.
• VirtualPool takes ~$10,070 worth of LP from the Rebalancing‑AMM (discounted).
• Removes that LP from Curve symmetrically -> gets ~0.053 wBTC + ~5,300 crvUSD.
• Repays 10,000 crvUSD of protocol debt; any leftover BTC (~0.112 wBTC) is the arb profit.
• Debt drops by 10k -> ratio back at ~50%.

End state
LP ≈ $179.9k, debt ≈ $90k -> debt / value ≈ 50%. Arb paid in BTC this time.

Who captures it? Any MEV/arb bot watching the Rebalancing‑AMM price. It’s atomic & oracle‑anchored, so it’s effectively risk‑free.

Where does profit come from? A small AMM spread plus a subsidy budget funded by recycled crvUSD borrow interest — not directly from LP principal.

3.3 How the Rebalancing‑AMM rebalances back to 50% (conceptual)

• If debt is below 50%, it quotes LP expensive in crvUSD -> arbs bring crvUSD, mint LP, debt rises.
• If debt is above 50%, it quotes LP cheap -> arbs pull LP out, repay debt.

An oracle‑anchored term ($x_0$) keeps the curve centered so trades naturally land at 50%.

Math reference: The invariant (x₀(p₀) − d) · y = I(p₀) and the closed‑form x₀ root are in Math Primer §3 (Eq. 5–6).

---

4. Borrowing & Interest Recycling (crvUSD line)

YieldBasis borrows crvUSD from its own, isolated CDP line on Curve. The interest it “pays” never leaves the system; it is fully used to rebalance the Curve Cryptoswap pool.

Interest Rate Recycling Flow: 100% of borrower interest is recycled into rebalancing the Cryptoswap pool. Pool fees are then split: 50% for pool rebalancing, 50% distributed between liquidity providers and dynamic admin fees (to veYB holders).

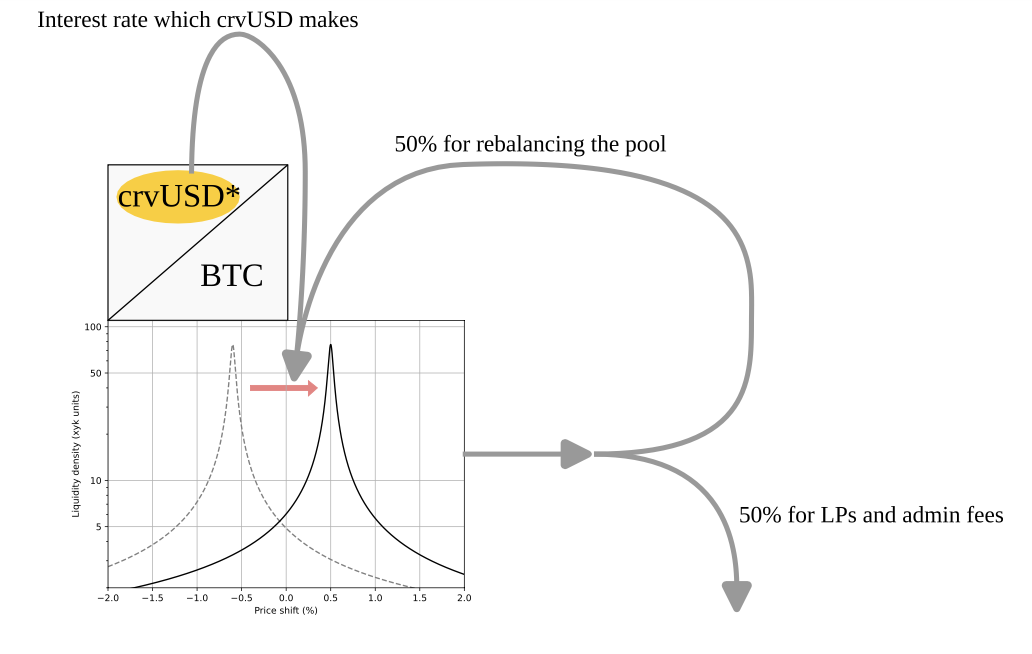
4.1 Dedicated crvUSD CDP Line

• Isolated market: The protocol mints/repays crvUSD against its LP collateral from a special crvUSD mint market, separate from public crvUSD borrowers. Only YieldBasis can borrow from this special market.
• Governance‑set rate: Curve/YB governance can tune the borrow APR specifically for leveraged liquidity use (doesn’t affect public CDPs and their borrow rates).

4.2 How Interest Is Captured

1. Debt accrues interest on the YB CDP (accounting-only increase in d).
2. When borrow rate fees are harvested (or on scheduled accounting ticks), the protocol “pays” that interest into an internal budget contract.
3. 100% of the crvUSD interest rate is recycled into rebalancing the Curve Cryptoswap pool.

Math reference: The net APR expression APR = 2·r_pool − (r_borrow + r_rebalancing) and its assumptions are in Math Primer §4 (Eq. 7).

4.3 Why It Matters — and What Can Go Wrong

Upsides

• No external lender bottleneck: Borrow capacity scales with LP collateral; no utilization spikes or liquidity shortages.
• Predictable leverage cost: Governance can smooth the borrow rate instead of exposing LPs to market swings.
• Self‑funding ops: Interest doesn’t leak; it powers rebalancing and protocol revenue.

Edge cases to watch

• Borrow rate too high: Net APR shrinks; governance must balance subsidy needs vs LP returns.
• Subsidy underfunded: The AMM difference narrows; rebalancing may lag or need wider quotes.
• crvUSD off‑peg: Debt is counted at $1 via oracle; deviations skew apparent leverage temporarily (see Risk §9).

More detail: Whitepaper's “Using CDP Interest Rate for Rebalancing” section and §6 Fee Split & Admin‑Fee Dynamics show how this budget flows to LPs and veYB.

---

5. Fee Split & Admin‑Fee Dynamics

YieldBasis LPs and veYB holders earn fees from the BTC/crvUSD pool trading activity. The fee distribution works as follows:

• 50% is recycled back into rebalancing the pool
• 50% is distributed between liquidity providers and veYB holders

YieldBasis uses a dynamic admin fee to balance incentives between liquidity providers and governance participants (veYB holders). This fee automatically adjusts based on staking levels to maintain optimal protocol balance.

5.1 Variables

• T — total ybBTC LP supply
• s — amount of ybBTC staked (earning YB emissions)
• f_min — minimum admin fee (e.g. 10%) when nobody stakes
• f_a — actual admin fee fraction taken from fees earned by the pool

5.2 Admin fee formula (intuitive form)

f_a = 1 - (1 - f_min) * √(1 - s/T)

Math reference: The admin‑fee function f_a = 1 − (1 − f_min) · √(1 − s/T) and the negative‑rebase formula δs are in Math Primer §5 (Eq. 8 and 5.6).

• If no one stakes (s = 0) -> f_a = f_min (LPs keep ~90% if f_min = 10%)
• If everyone stakes (s = T) -> f_a -> 100% (all fees diverted to veYB since LPs chose emissions instead)
• In between -> fee ramps up smoothly and non‑linearly

5.3 Flow of value

1. Pool fees accrue on the BTC/crvUSD Curve LP.

2. YieldBasis harvests those fees -> splits them:

   • f_a portion -> veYB (admin fee)
   • (1 - f_a) portion -> unstaked ybBTC as BTC-denominated yield

3. Staked ybBTC do not receive fees; they receive YB emissions instead.

Stake choice	Receives	Forfeits
Unstaked ybBTC	BTC fees (1 - f_a)	YB emissions
Staked ybBTC	YB emissions	BTC fees
veYB (locked YB)	Admin fee f_a	Liquidity of YB

5.4 Game theory intuition

As more LPs stake for YB rewards, the admin fee approaches toward 100% and the fee pool for unstaked LPs shrinks. However, with so few unstaked LPs remaining, each receives a proportionally larger share of that smaller pool.

• Set f_min too high: Unstaked LPs might flee; yields look unattractive.
• Set f_min too low: veYB value capture shrinks; weak governance incentive.

Sudden stake/unstake swings: Fees redistribute next epoch; protocol must handle rebases for staked supply (negative rebases described in the whitepaper).

5.5 Regarding the APRs of ybBTC and st-ybBTC

It was previously claimed that when $f_a$ increases, the unstaked ybBTC holders still extract meaningful yield. It is now to be shown. Consider that a quantity of $s$ ybBTC had been staked, and the total distributable income and the total quantity of ybBTC are both unity. Then:

$f_a = 1-(1-f_{min})\sqrt{1-s}$

The yield to ybBTC holders is: $ybBTC_\text{yield} = (1-f_{min})\sqrt{1-s}$

This quantity is distributed to $1-s$ ybBTC units. Then the marginal yield has a dependency of the form

$ybBTC_\text{yieldMarginal} = \frac{(1-f_{min})\sqrt{1-s}}{1-s} = \frac{1-f_{min}}{\sqrt{1-s}}$

With a derivative w.r.t $s$ of

$d_s \times ybBTC_\text{yieldMarginal} = \frac{1-f_{min}}{2(1-s)^{3/2}}$

It is now observed that the derivative is positive for any admissible value of $s$, which means that the APR of ybBTC indeed grows together with $f_a$ and incentivises ybBTC retention when the latter shrinks.

If the quantity of veYB were kept constant, a very similar observation would hold for veYB; it does not entirely hold precisely because of the liquidity-mining emissions.

Moreover, a similar consideration for liquidity-mining shows that it loses in marginal effeciency as more ybBTC is staked, also because the emission scales as a square root, and the quantity of recipients scales linearly.

For $s$ staked ybBTC and a total ybBTC of unity:

$E_{daily} = E_{max}\sqrt{s}$

$E_\text{daily,marginal} = \frac{E_{max}\sqrt{s}}{s} = \frac{E_{max}}{\sqrt{s}}$

$d_s \times E_\text{daily,marginal} = -\frac{E_{max}}{2s\sqrt{s}}$

Observe that this derivative is negative for all admissible $s$. It then follows that an increased collective investment in liquidity mining both provides diminishing returns and increases the APR of the remaining ybBTC, which helps preventing the system from collapsing into one of the two extreme states (either all staked or all unstaked), with the precise equilibria being determined by the quantity and price of veYB, which is exogenous to the above considerations.